September 24, 2025 @ 21:55
Solving Hungarian Rings

pic from Wikipedia
I took a break from studying maths today to think about other maths. Wild, I know.
Actually I thought I'd attack an interesting puzzle: Hungarian Rings. I didn't use the physical version of it. Instead I downloaded this program, which is pretty good. I made the pics for this article by taking screenshots from that program.
I wondered how to solve it, so I wrote down some notation:
Let:
$$ L $$ be a clockwise turn of the left ring $$ L' $$ be anticlockwise $$ R $$ be a clockwise turn of the right ring $$ R' $$ be anticlockwise
The puzzle looks like this when solved, but usually without numbers:
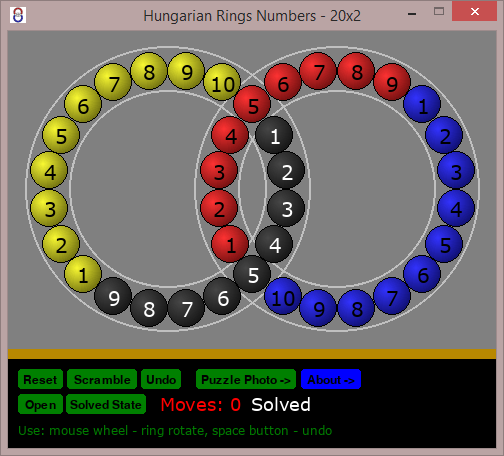
When I solve a twisty puzzle like this one, I generally try to find algorithms that affect just a few pieces at a time. That way, you can make progress in one area without ruining your gains elsewhere.
Some maths
Firstly, we should understand the notation: any $$ X' $$ is the inverse of the algorithm $$ X $$ If $$ X = R L L' $$ then $$ X' = L L' R' $$ In other words, the inverse of an algorithm is the opposite steps in the opposite order. To say $$ X X' $$ means we end up where we started, otherwise known as the neutral element. In our case, the neutral permutation for this puzzle is just the current state of the puzzle.
A commutator is any move in the form $$ X Y X' Y' $$ A conjugate is any move in the form $$ X Y X' $$ Note that in this scheme, $$ X $$ and $$ Y $$ could be any ordered sequence of $$ \{R, L, R', L'\}$$ , including multiples. Essentially, commutators do useful things to a permutation puzzle, while conjugates allow you to use a useful commutator in more places. This is probably best explained with pictures (see below).
This puzzle has permutations that are always even and we can understand any permutation as being the combination of an event number of disjoint swaps. So, if we find a move that has two swaps then that's the best we can do. This is an interesting video about why this puzzle has permutations of even parity: https://www.youtube.com/watch?v=w0mxdo5ur_A . But essentially, since every spin of a ring puts 20 balls in a cycle, or 4 balls in 5 cycles etc, then it's always an even number of swaps.
Some attempts
Firstly, some of the results I find are overkill, since swapping two balls of the same colour has no consequence in the standard version of the puzzle. The harder version has numbers so I'll persist with that.
Let $$ A = L' R L R' $$ be a commutator. I started with this because I knew it would be a useful pattern, having used these to solve other permutation puzzles.
The result of $$ A $$:
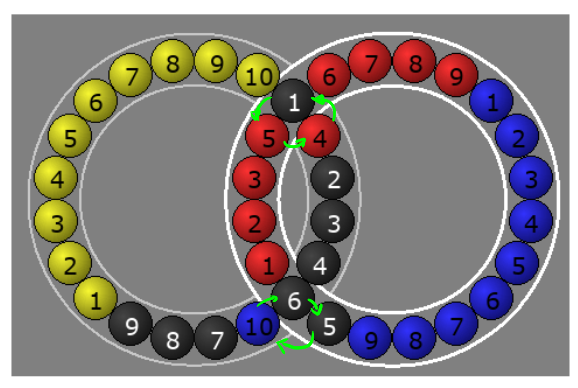
As you can see, this results in two disjoint 3-cycles. In the numberless version of Hungarian Rings, this is effectively an algorithm that swaps a red with a black and another black with a blue, since replacing a black with a black, or a red with a red, doesn't matter.
The commutator $$A$$ could be more useful, so I tried making it part of a larger commutator:
$$ \begin{matrix}R \\ A \\ R' \\ A' \end{matrix} \space = \begin{matrix} R \\ L' R L R' \\ R' \\ R L' R' L \\ \end{matrix} \space = \space \begin{matrix} R \\ L' R L R' \\ L' R' L \\ \end{matrix} $$
Note that the third version of the same algorithm contained $$ R * R' $$, which cancels. In algebra we say it equals the neutral element, but we can say it cancels.
This improved algorithm results with the permutation here:
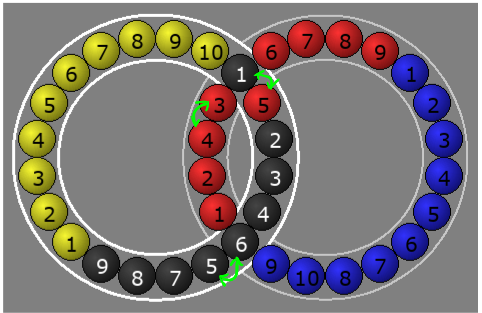
So, we end up with four swaps (forgot to highlight (9,5)$$ I decided this series of attempts had gone cold so I moved on.
I made a new commutator to see what else I could find:
$$ B = R L' R' L $$
And for interest's sake, did $$ B R $$ .
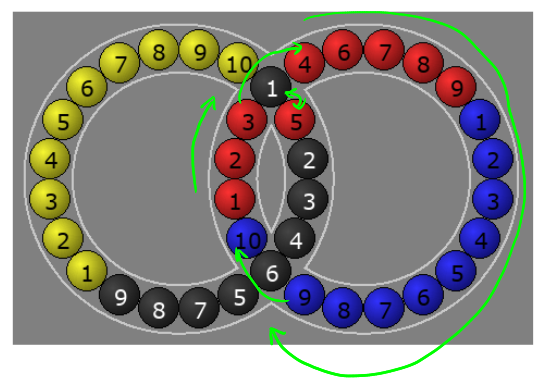
This one is interesting. The entire right ring spins clockwise, except for black 6, so blue 10 jumps one. The other ring doesn't move except that red 5 switches with black 1.
So I tried set this up as a conjugate cycle:
$$ L B R L' $$
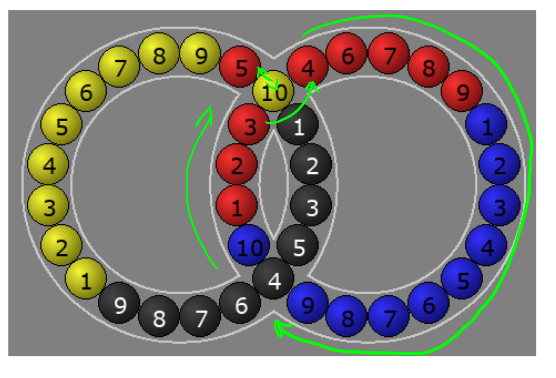
But decided dropping the L' was more useful:
$$ L B R $$
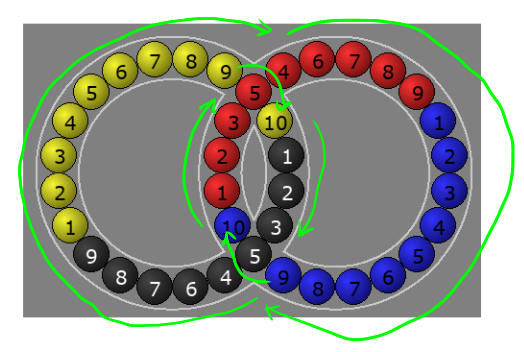
So, this causes each ring to spin clockwise, except for the red 5 and black 5, which each stay put. I thought that was pretty cool, so I assigned:
$$ C = L B R = L R L' R' L R $$
And I tried some more stuff. It seems to me that mathematics is mostly trying stuff, and seeing what sticks, and solving puzzles is a very mathy thing to do with your time.
I eventually found:
$$ \begin{matrix} L' \\ C \\ L \\ C' \\ \end{matrix} \space = \space \begin{matrix} L' \\ L R L' R' L R \\ L \\ R' L' R L R' L' \\ \end{matrix} \space = \space \begin{matrix} R L' R' L R \\ L \\ R' L' R L R' \\ L' \\ \end{matrix} $$
If we let $$ D = R L' R' L R $$ then
$$ \begin{matrix} L' \\ C \\ L \\ C' \\ \end{matrix} \space = \space \begin{matrix} D \\ L \\ D' \\ L' \\ \end{matrix} $$
The result is:
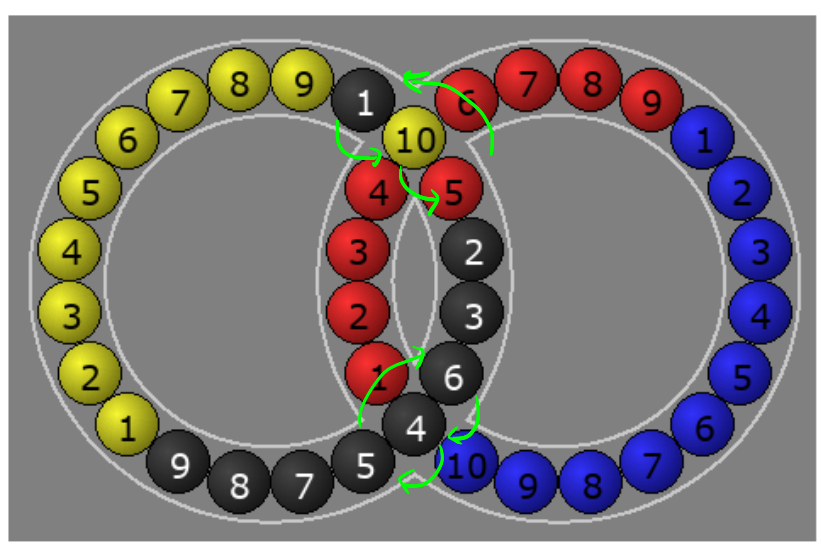
Which is two disjoint 3-cycles. That's useful to have.
Then I noticed that if you rotate the left ring by 5 spaces, and then the right ring by 5 spaces, the red 5 doesn't actually move.
So let there be a new commutator $$ E = 5L \space 5R \space 5L' \space 5R' $$
And we now have:
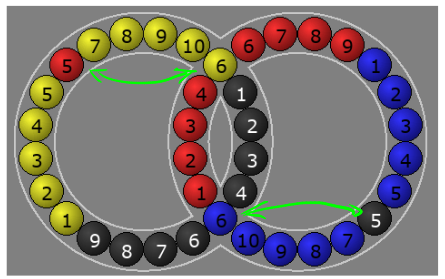
Now that we've found an equation with two swaps, we can say this is as good as it gets. This puzzle will never have a permutation that is 1, 3, 5 etc swaps different from the solved state. So this is the algorithm we can now use to solve the puzzle since this is the one that will allow us to avoid making a mess elsewhere.
But to make it more useful, we can still use a conjugate cycle:
Let $$ F = R' L' R L $$
Then if you do: $$ F E F' $$ you get:
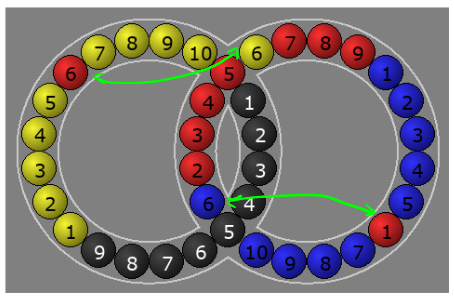
Or $$ F' E F $$, you get:
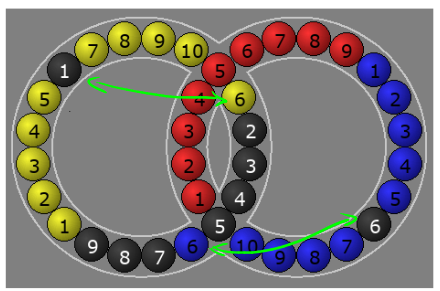
You could also do something like:
$$ H = 4L \space 4R \space 4L' \space 4R' $$, where $$ 4L $$ is a clockwise spin of the left ring that moves $$ 4 $$ balls over.
Then $$ H E H' $$
Will get you this:
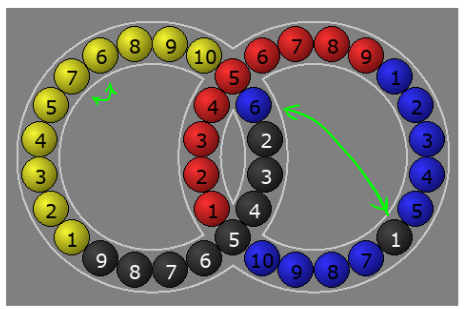
And so on. This is how I solve twisty puzzles. I've never looked at the algorithms that others have made, but I don't need to, since this process can be used to solve essentially any permutation puzzle. I've used it for Rubik's Cube, other cubes, Megaminx, etc.